La formula del delta (Δ) in matematica
Formula delta: come si calcola e a cosa serve il Δ
La formula delta, indicata con il simbolo Δ, è uno strumento fondamentale per risolvere le equazioni di secondo grado. In questa guida scoprirai cos'è il delta, come si calcola e a cosa serve nei diversi casi.
In matematica la formula del Δ è anche conosciuta come formula del discriminante.
Qual è la formula del delta (Δ)?
La formula del delta si utilizza per determinare le soluzioni delle equazioni di secondo grado in forma normale:
Δ = b² - 4ac
Come si calcola il delta in modo semplice?
Consideriamo l’equazione di secondo grado generica:
ax² + bx + c = 0
Il calcolo del delta consiste nel fare il quadrato del coefficiente b (quello di primo grado) meno il quadruplo del prodotto tra il coefficiente a (di secondo grado) e il termine noto c:
Δ = b² - 4ac
Calcola il delta (Δ) online
A cosa serve il delta nelle equazioni di secondo grado?
Il valore di Δ ci dice quante e quali soluzioni ha l'equazione:
- Δ > 0: due soluzioni reali e distinte.
- Δ = 0: due soluzioni reali e coincidenti.
- Δ < 0: nessuna soluzione reale (soluzioni complesse).
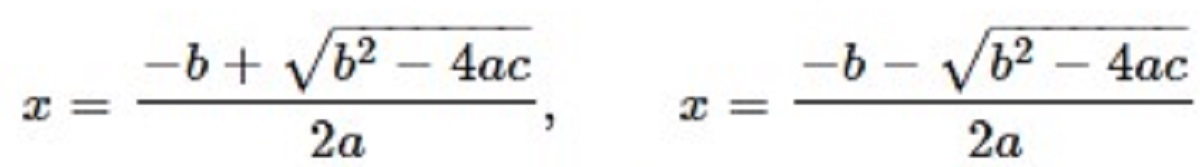
Esempio pratico: quando serve davvero il delta nella vita?
Immagina di lanciare una palla verso l’alto da un’altezza di 2 metri. Vogliamo sapere dopo quanti secondi la palla toccherà terra.
Ecco l’esempio:
Dati:
- Altezza iniziale: 2 metri
- Velocità iniziale: 6 m/s
- Accelerazione di gravità: −9,8 m/s²
L’altezza nel tempo è data dalla formula:
h(t) = -4,9t² + 6t + 2
Per scoprire quando la palla tocca terra, poniamo h(t) = 0:
-4,9t² + 6t + 2 = 0
Questa è un’equazione di secondo grado! Applichiamo la formula del delta:
Δ = 6² - 4 × (-4,9) × 2 = 75,2
Risolvendo con la formula:
t = (-6 ± √75,2) / (2 × -4,9)
Il tempo positivo (cioè reale) è circa 1,5 secondi. Questo è quando la palla torna a terra!
Video: sulla Luna, anche una piuma cade come un martello. La gravità agisce ugualmente su tutto!
Perché si chiama "discriminante"?
Il termine discriminante si riferisce al fatto che il valore del delta discrimina (cioè distingue) tra i vari casi possibili di soluzioni.
Curiosità su b² - 4ac
Se ti interessa approfondire, ti consiglio questo articolo su amicoprof.it ricco di curiosità sulla formula del delta.
Video tutorial sulla formula del delta
Scopri il significato pratico e geometrico della formula delta con questo simpatico video di Schooltoon:
E se vuoi esercizi guidati sulla formula Δ e varianti come il "delta quarti", ecco un’altra risorsa utile: